The Power of Compounding and Rule of 72: Understanding Exponential Growth in Personal Finance

-

"Compound interest is the eighth wonder of the world. He who understands it, earns it ... he who doesn't ... pays it." - Albert Einstein

"The power of compounding is the most powerful force in the universe." - Albert Einstein

"The greatest shortcoming of the human race is our inability to understand the exponential function." - Al Bartlett

The power of compounding is the ability of an investment or savings to grow exponentially over time, as the returns generated by the investment are reinvested to generate further returns. In other words, compounding allows you to earn interest on both the principal amount and the accumulated interest.

Here's a simple example to illustrate the power of compounding:

Suppose you invest Rs.1,000 in a savings account that pays 5% interest per year, compounded annually. After one year, your investment would have grown to Rs. 1,050 (Rs. 1,000 x 1.05). If you leave your investment untouched for another year, it would grow to Rs. 1,102.50 (Rs. 1,050 x 1.05), and so on.

After 10 years, your initial investment of Rs. 1,000 would have grown to Rs. 1,628.89, and after 20 years, it would have grown to Rs. 2,653.30. This is due to the compounding effect, where the interest earned on your investment is reinvested to generate further interest.

The formula to calculate the future value of an investment using compounding is:

FV = PV x (1 + r/n)^(n x t)

Where:

FV = Future Value

PV = Present Value (or the initial investment)

r = Annual Interest Rate

n = Number of times interest is compounded per year

t = Time (in years)


In the example above, the values would be:

PV = Rs. 1,000

r = 5%

n = 1 (since the interest is compounded annually)

t = 10 years

Using the formula, we can calculate the future value of the investment:

FV = Rs. 1,000 x (1 + 0.05/1)^(1 x 10)

FV = Rs. 1,628.89

As you can see, compounding can have a significant impact on the growth of an investment over time, making it a powerful tool for building long-term wealth.


The rule of 72 is a simple mathematical formula that helps you estimate how long it will take for your investments to double, based on the interest rate or rate of return you are earning.

The formula for the rule of 72 is:

Number of years to double = 72 / Interest rate or rate of return

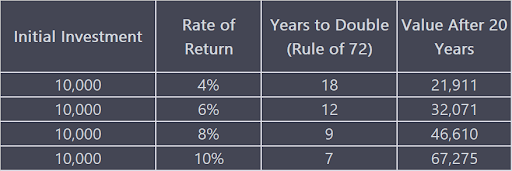
For example, if you are earning a 6% rate of return on your investments, the rule of 72 would suggest that it would take approximately 12 years for your investments to double in value (72 / 6 = 12).


Here's a real-life example to illustrate the rule of 72:

Suppose you have Rs. 10,000 to invest and you earn an average annual return of 8% on your investment. Using the rule of 72, you can estimate that it would take approximately 9 years for your investment to double in value (72 / 8 = 9).

So, after 9 years, your Rs. 10,000 investment would have grown to Rs. 20,000. If you leave your investment untouched for another 9 years, it would double again to $40,000, thanks to the power of compounding.

The rule of 72 can be a useful tool for evaluating different investment opportunities and estimating the potential growth of your investments over time. It can also help you understand the impact of fees, taxes, and inflation on your investments, as these factors can affect your overall rate of return.

The power of compounding is what makes the rule of 72 work. By reinvesting your earnings and allowing your investment to grow over time, you can potentially double your investment value in a shorter amount of time.

For example, if you invest Rs. 10,000 at an annual rate of return of 8%, the rule of 72 tells us that it will take approximately 9 years for your investment to double in value. However, if you reinvest your earnings and allow your investment to compound over time, you may be able to achieve this growth even faster.

Tabular illustration of rule 72 & power of compounding


In summary, the rule of 72 and the power of compounding are both important concepts in personal finance and investing. The rule of 72 can help you estimate the potential growth of your investments, while the power of compounding can help you achieve exponential growth over time by reinvesting your earnings.

Further Reading:

1. Effective Personal Finance Management in India 2023: Tips on Budgeting, Investing, Life & Health Insurance and More

Location: India

Comments

Post a Comment

Popular posts from this blog

Government Employee's Guide to Millionaire Status: 6 Proven Steps for Wealth Building through Personal Finance

-
Image
Becoming a millionaire as a government employee is possible with a disciplined and long-term approach to personal finance. There is always a misconception that only business magnets can become millionaires.  Here are some steps that can help a government employee become a millionaire: 1. Start with a Financial Plan: The first step towards becoming a millionaire is to create a financial plan that includes setting financial goals and a budget . This plan should take into account the employee's current income, expenses, and debt .   For example, a government employee earning Rs. 6,00,000 a year may set a goal to save Rs. 1,00,000 a year towards retirement. They can create a budget that allows for living expenses, debt payments, and saving Rs.8333 a month towards retirement. 2. Save and Invest Consistently: Saving and investing a portion of one's income consistently over time is key to building wealth. As a government employee, one can take advantage of retirement plans suc...
Read more

7 Financial and Health Benefits of Joining Zumba Dance Classes for a Fun Fitness Experience

-
Image
"Ditch the workout, join the party!" - Zumba Fitness Zumba is a popular form of aerobic exercise that combines dance and fitness. It was first created in the 1990s in Colombia and has since spread to become a global phenomenon. Zumba dance classes are popular with people of all ages and fitness levels, and they provide a range of monetary and economic benefits.  So, Are you looking for a fun and effective way to improve your health and finances at the same time? Look no further than Zumba dance classes! Not only is Zumba a great way to burn calories and stay fit, but it can also offer a range of financial benefits that can improve your overall financial wellness. In this article, we'll explore the top 7 financial and health benefits of joining Zumba dance classes. 1. Weight loss and health benefits One of the most significant monetary and economic benefits of joining Zumba dance classes is weight loss and improved health. Zumba is a high-energy aerobic workout that burns ...
Read more

Effective Personal Finance Management in India 2023: Tips on Budgeting, Investing, Life & Health Insurance and More

-
Image
Managing personal finance in India in 2023 requires a careful consideration of both macroeconomic and microeconomic factors. Here are some tips to help you manage your personal finances effectively in 2023: 1. Start by creating a budget:  "A budget is telling your money where to go instead of wondering where it went." - Dave Ramsey A budget is a crucial tool that helps you track your expenses and identify areas where you can cut costs. Make sure to include all your sources of income and expenses, including fixed and variable expenses. Stick to your budget as much as possible to ensure you're spending within your means. 2. Save and invest:   "The stock market is a device for transferring money from the impatient to the patient." - Warren Buffett With inflation likely to remain high in 2023, it's important to save and invest wisely. Consider investing in assets such as stocks, mutual funds, or real estate that have a potential for high returns. However, it...
Read more